Dans de très nombreux cas, surtout lorsqu’on aborde l’intégration, on a besoin de savoir diviser des polynômes :
$$ \dfrac{x^3 -5x^2 +7x -9}{x-4} = x^2 -x + 3 + \dfrac{3}{x-4}$$
Algorithme de la division
Si \( f(x) \) et \( d(x) \) sont des polynômes tels que \( d(x) \ne 0 \), et le degré de \( d(x) \) est
inférieur ou égal au degré de \( f(x) \), alors il existe des polynômes uniques
\( q(x) \) et \( r(x) \) tels que :
$$\begin{align*} f(x) = d(x)q(x) + r(x) \end{align*} $$
$$\begin{array}
{ll} f(x) \textrm{ : dividende } & d(x) \textrm{ : diviseur } \\
q(x) \textrm{ : quotient } & r(x) \textrm{ : reste }
\end{array}
$$où \( r(x) = 0\) ou le degré de \( r(x) \) est inférieur au degré de \( d(x) \)
Une autre forme : \( \dfrac{f(x)}{d(x)} = q(x) + \dfrac{r(x)}{d(x)} \)
Division longue (euclidienne)
Pour la division longue, peu de mystères, division euclidienne classique.
Diviser \( \dfrac{x^3 -5x^2 +7x -9}{x-4} \)
$$ \begin{array}
{rrrr|ll} x^3 & -5x^2 & +7x & -9 & x - 4 \\ \hline
-x^3 & +4x^2 & & & x^2 - x + 3 \\
& -x^2 & +7x & -9 & \\
& x^2 & -4x & & \\
& & +3x & -9 & \\
& & -3x & +12 & \\
& & & +3 & \\
\end{array}
$$\( \implies \dfrac{x^3 -5x^2 +7x -9}{x-4} = x^2 - x + 3 + \dfrac{3}{x-4} \)
Ajouter les termes manquants si nécessaire pour appliquer l’algorithme.
Diviser \( \dfrac{x^3 - 1}{x-1} \)
$$ \dfrac{x^3 - 1}{x-1} = \dfrac{x^3 + 0x^2 + 0x - 1}{x-1} $$
$$\begin{array}
{rrrr|l} x^3 & +0x^2 & +0x & -1 & x - 1 \\ \hline
-x^3 & +x^2 & & & x^2 + x + 1 \\
& +x^2 & +0x & -1 & \\
& -x^2 & +x & & \\
& & +x & -1 & \\
& & -x & +1 & \\
& & & 0 & \\
\end{array}
$$\( \implies \dfrac{x^3 - 1}{x-1} = x^2 + x + 1 , \ x \ne 1\)
Diviser :
\( \displaystyle { \dfrac{2x^4 + 4x^3 -5x^2 + 3x - 2}{x^2 +2x -3} }\)
\( \displaystyle { \dfrac{2x^4 -x^2 - 2}{x^2+2x-1} }\)
Division synthétique
Pour des divisions longues de polynômes par des diviseurs de la forme \( x - k \), il y a un raccourci pratique : la division synthétique.
Pour diviser \( ax^3 + bx^2 + cx + d \) par \( x- k \), utiliser ce schéma :
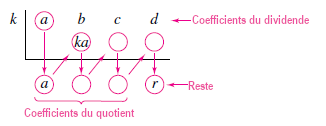Dans les verticales : addition des termes
Dans les diagonales : multiplication par \( k \)
Dans les verticales : addition des termes
Dans les diagonales : multiplication par \( k \)Cet algorithme de la division synthétique fonctionne uniquement pour les diviseurs de la forme \( x -k\), mais il suffit de se rappeler que \( x + k = x - (-k) \).
Le schéma pour des polynômes de degré plus élevé est le même. Inclure \(0\) pour les termes \( x^n\) manquants.
\( \dfrac{x^4 −10x^2 −2x + 4}{x+3} \)
$$\begin{align*}
\begin{array}{c|rrrrr}
& x^4 & x^3 & x^2 & x^1 & x^0 \\
& 1 & 0 & -10 & -2 & 4 \\
{\color{red}-3} & & -3 & +9 & +3 & -3 \\
\hline
& 1 & -3 & -1 & 1 &|\phantom{-} {\color{blue}1}
\end{array}
\end{align*}
$$
\( \implies \dfrac{x^4 −10x^2 −2x + 4}{x+3} = x^3 -3x^2 -x + 1 + \dfrac{1}{x+3}\)
Diviser par une division synthétique :
\( \displaystyle { \dfrac{5x^3 + 8x^2 −x + 6}{x+2} }\)